The MAUP Effect: Spatial Scale and the Reliability of Segregation Indices

Research note

---

Abstract

This research note examines the implications of the modifiable areal unit problem (MAUP) for the measurement of ethnic segregation in Hamburg, Germany, utilizing 2011 census data and a simulation-based approach that incorporates 10 distinct spatial operationalizations. The results indicate that spatially adjusted global segregation estimates demonstrate a marked resilience to MAUP, despite the correlations between German and foreign populations exhibiting pronounced volatility, which undermines the reliability and comparability of the findings. Moreover, local segregation measures are found to be acutely sensitive to scale and zoning choices, particularly in areas distinguished by heterogeneous distributions of characteristics. In contrast, regions exhibiting homogeneous distributions of characteristics demonstrate consistent measurement outcomes across operationalizations. To mitigate the effects of MAUP, an MAUP-robust segregation index can be estimated to provide a coarse quantification of the distorting effects of MAUP on local and global measurements, as demonstrated in Hamburg and Munich, with partial feasibility. Moreover, theoretical knowledge must inform the operationalization of spatial layout, as MAUP is fundamentally a theoretical problem. This underscores the imperative need for rigorous theoretical justification of the spatial frameworks employed in segregation research.

Keywords

aggregation, MAUP, modifiable areal unit problem, segregation, spatial analysis

Acknowledgement

Acknowledgements: I would like to extend my sincere gratitude to the anonymous reviewer and the editor for their thoughtful and constructive comments, which significantly improved the quality of this research note. Their guidance and expertise were invaluable in refining my arguments and presentation.

Introduction

This research note examines the modifiable areal unit problem (MAUP) and its potential to distort the measurement of segregation indices. First identified by Openshaw and Taylor (1979) and Fotheringham and Wong (1991), ‘MAUP’ refers to the sensitivity of analytical and descriptive results to the chosen spatial scale or zoning of spatial data. The accurate quantification of segregation is crucial for developing evidence-based policy interventions (Reardon & O’Sullivan, 2004). The pervasiveness of MAUP necessitates caution when analyzing and interpreting analytical results based on aggregated spatial data, as MAUP poses a significant threat to the validity of comparisons across analytical results.

To investigate the severity of MAUP in segregation measurement, I conducted a simulation study using fine-grained, geocoded data from the German Federal Statistical Office (2018). Focusing on the impact of MAUP on global and local segregation measures, I analyzed 10 distinct spatial scales and zoning configurations. Employing a simulation-based approach (Amrhein, 1995), I generated 10,000 random geocoordinates within Hamburg’s inhabited area, simulating real-world scenarios and facilitating a systematic examination of MAUP’s impact on segregation indices. The findings of this research note highlight the need for a paradigmatic shift in understanding MAUP as a fundamental theoretical concern, rather than a mere technical issue. This research is intended to inform a dual-pronged approach to addressing MAUP, comprising both theoretical frameworks and technical strategies for mitigation.

What is the modifiable areal unit problem (MAUP)?

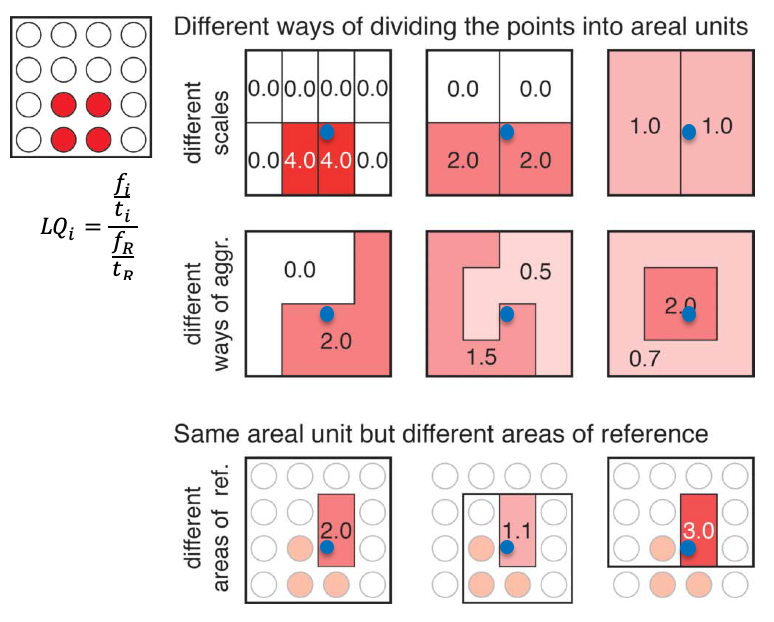
MAUP poses a pervasive methodological challenge in spatial analysis, with far-reaching implications. It arises when point-level data are aggregated into spatially defined areas, such as neighbourhoods, districts, or other areal units, which introduces scalability and zoning effects that can significantly influence analytical outcomes. This phenomenon is succinctly illustrated in Figure 1, which depicts the location quotient calculated using diverse spatial operationalizations (Hennerdal & Nielsen, 2017). The location quotient, defined as the ratio of red dots within each unit ( f_i/t_i ) relative to the reference unit ( f_R/t_R ), is calculated for each operationalization.

As a segregation index, the location quotient compares aggregated information from a spatial unit with that of a reference spatial unit. Figure 1 illustrates how the same point pattern yields divergent location quotient values when aggregated at different spatial scales and zoning configurations, which exemplify the MAUP effect.

 

Figure 1: Variation of location quotients by spatial scale and zoning

A visual representation of the results, such as colour-coded areas, is less accurate due to the inherent instability of the location quotient. Moreover, the location quotient of a hypothetical household (blue dot) exhibits significant fluctuations when rescaling or re-zoning occurs – a phenomenon that can be exploited in gerrymandering (Engstrom, 2013). MAUP is also contingent on the zoning or scaling of the areal unit of reference, which is a crucial yet often overlooked consideration (Hennerdal & Nielsen, 2017). This underscores the far-reaching theoretical implications of MAUP, which challenge the assumption that different spatial scales or zones can provide a consistent picture of individual situations. Echoing the ecological fallacy (Wong, 2004), MAUP cautions against inferring individual situations from aggregated data. Rescaling or re-zoning can have unpredictable effects on simple measures, such as the location quotient, mean, and correlation, which are then further exacerbated in multivariate analyses (Fotheringham & Wong, 1991; Wong, 2004). This uncertainty compromises the reliability, meaningfulness, and comparability of analytical results based on aggregated spatial data. While the use of geocoded point data in segregation studies has been proposed as a potential solution (Arribas-Bel et al., 2016; Reardon & O’Sullivan, 2004), the challenge of generating meaningful spatial units persists.

Data and methods

The European Union’s decennial population census provides aggregated data with a fixed scope of characteristics (Destatis, 2018). The 2011 census data, available at a 100 x 100-meter grid resolution, enable fine-scale spatial analysis that transcends administrative boundaries (BKG, 2017), facilitating comparative studies at the European level (e.g. Andersson et al., 2018; Costa & De Valk, 2018). Census-derived data on German residents and foreigners were spatially joined to multiple overlaying layers, including suburb, postcode area, and district (LGV, 2016). From the fine-grained data, varying grid scales (ranging from 100 x 100 metres to 600 x 600 metres) were generated to calculate both global and local measures of ethnic segregation in Hamburg. The distinction between micro- and macro-segregation is crucial, as research suggests they represent distinct spatial separation processes (Lichter et al., 2015).

Global segregation coefficients were calculated to capture varying dimensions of segregation (Duncan & Duncan, 1955; Meister & Niebuhr, 2020). Additionally, correlations between German and foreigner populations were calculated, providing insights into the potential biasing effects attributable to MAUP (Fotheringham & Wong, 1991).

Global segregation indices

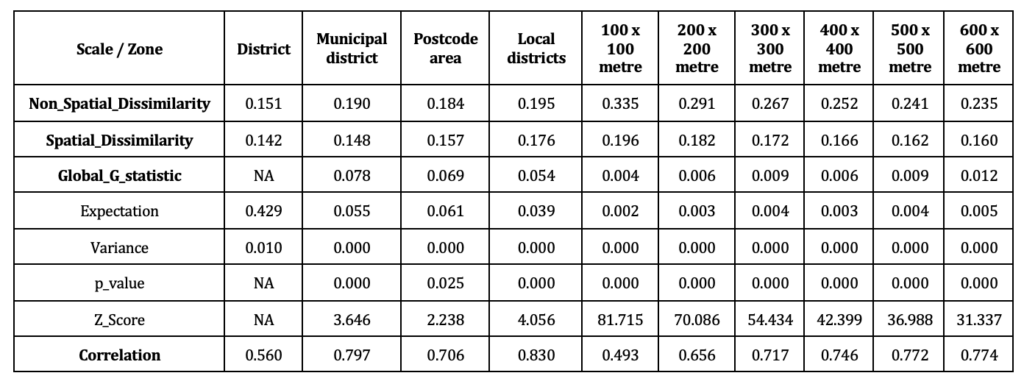
I computed multiple global segregation indices for the city’s 10 distinct spatial divisions, acknowledging the influences of MAUP and the measurement type (Meister & Niebuhr, 2020, p. 45). Specifically, I calculated non-spatial and spatial dissimilarity indices. In addition, I computed the global Getis-Ord index (Getis & Ord, 2010), which captures clustering patterns and yields a global indication of spatial autocorrelation, with p-values and Z-values serving as the primary foci of interpretation. While other global segregation indices exist (Hong et al., 2014), many are susceptible to MAUP challenges and share similar calculation structures.

Local segregation index

To quantify the local segregation, I calculated the location quotient for 10,000 geocoordinated fictional households across Hamburg’s 10 spatial divisions. This metric revealed the concentration of foreign-born individuals, with values greater than 1 indicating higher-than-average concentrations and values less than 1 indicating lower-than-average concentrations.

Results

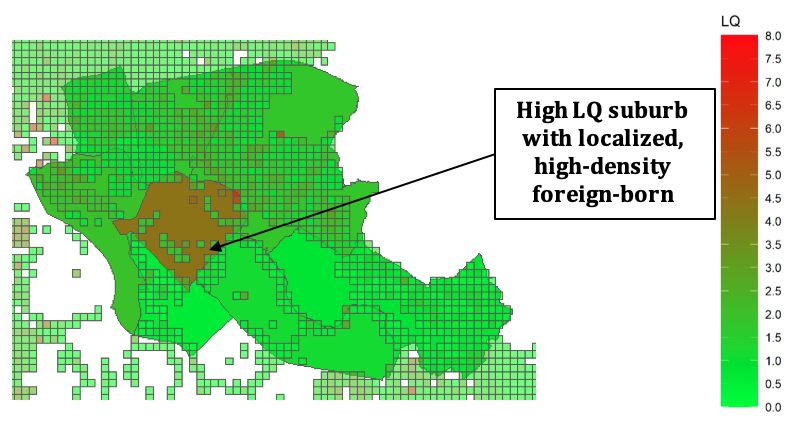
The visual representation in Figure 2 illustrates the susceptibility of interpretation to changes in spatial configuration, with divergent results obtained using 200 x 200-metre grid data versus suburban-level data. Notably, suburban-level segregation patterns are revealed – upon closer examination of the grid data – to be misinterpretations, where high segregation values are confined to a limited number of grid cells. The uneven spatial distribution of the two groups often transcends district boundaries, resulting in distorted segregation patterns (the so-called ‘chessboard problem’ ]) and exhibiting pronounced sensitivity to the scale and zoning of areal units of analysis.

 

Figure 2: Suburb vs. 200 x 200 m Grid: Spatial Operationalizations Compared

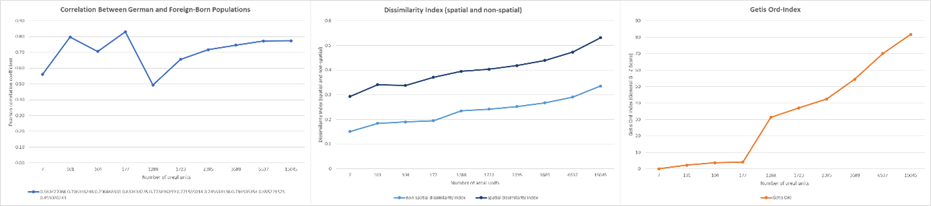
Figure 3 and Table 1 illustrate the spatial scale-dependent variability in correlations between the number of Germans and the number of foreigners, which undermines the foundation of statistical methods that rely on correlations (Wong, 2004, 2009). This inconsistency has significant implications for multivariate analyses, as highlighted by Fotheringham and Wong (1991). Spatial scale exerts a profound impact on the analysis of ethnic segregation, where more-aggregated units exhibit stronger correlations, and disaggregated units display weaker correlations, consistent with prior empirical and theoretical findings (Clark & Avery, 1976; Fotheringham & Wong, 1991).

As a result, MAUP presents a significant challenge to the comparison of analytical results, as varying spatial scales and zoning configurations can yield divergent conclusions regarding the same phenomenon. For example, an analysis conducted at the neighbourhood level may suggest a strong correlation between the number of Germans and foreigners, whereas the same analysis conducted at a spatial resolution of 500 x 500 metres may reveal a substantially weaker correlation. Furthermore, the sensitivity to spatial scale and zoning configuration extends to the calculation of spatial and non-spatial dissimilarity indices, which compromises the validity of comparisons across analytical results.

 

Figure 3: Scaling Effects on Correlation Coefficients, Dissimilarity, and Getis-Ord Index

The global ethnic-segregation index exhibits spatial scale dependence, conforming to Tobler’s first law of geography (Tobler, 1970). Similarly, the global Getis-Ord Index (Getis & Ord, 2010) displays spatial scale dependence. Notably, my results reveal that advanced versions of the simple dissimilarity index, such as those proposed by Meister and Niehbuhr (2020), exhibit greater robustness to MAUP.

 

Table 1: Overview of coefficients of the 10 operationalisations of the spatial units

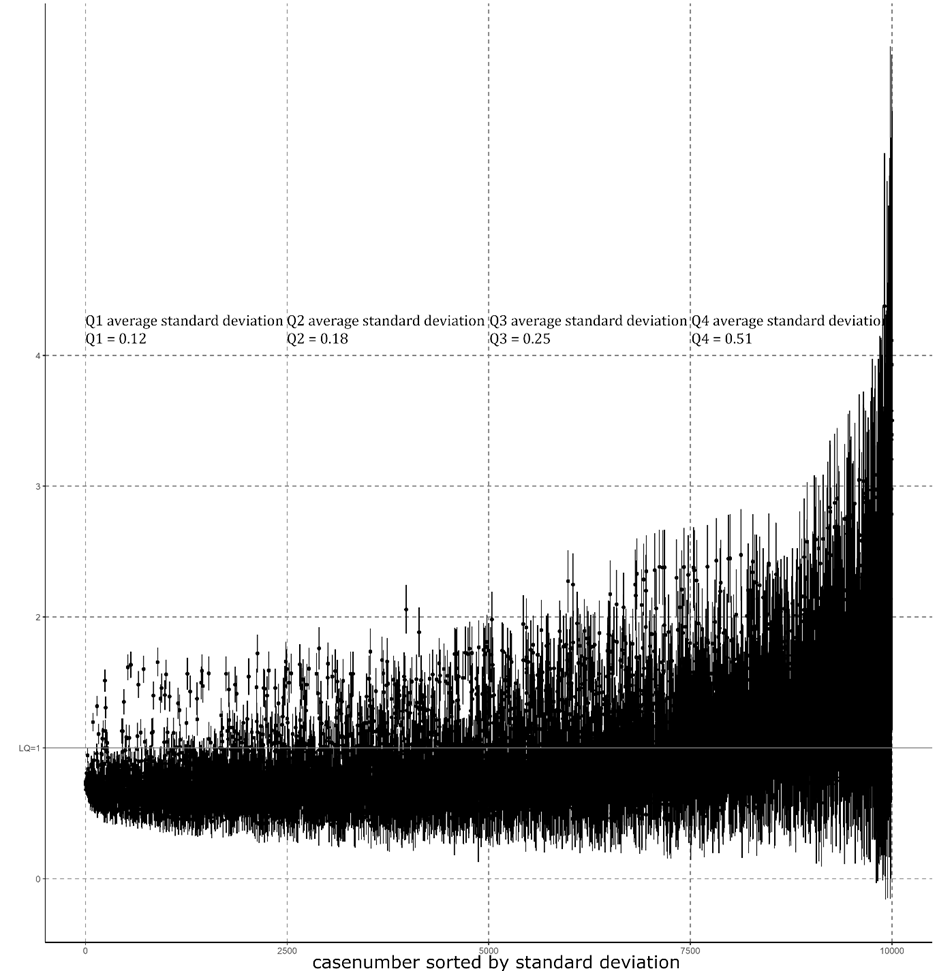
The local segregation index, operationalized as ‘location quotient’, exhibits considerable variation, with a standard deviation of 0.12 in the most consistent cases (1st quartile) and 0.51 in the most inconsistent cases (4th quartile), indicating high sensitivity to spatial layout (Figure 4). A high standard deviation can substantially impact the interpretation of the location quotient, particularly when the variance of measurement results exceeds or falls below 1. Notably, 38.03% of geocoordinates exhibit changed interpretations, with 77% of these cases concentrated in the third and fourth quartiles. This variability raises concerns about the reliability and robustness of descriptive results, limiting the ability to generalize findings or identify patterns across different spatial layouts. Specifically, the variance in measurement can be interpreted as measurement error, which has well-documented implications, including wider confidence intervals for variables and significant impacts on p-value interpretation (Fotheringham & Wong, 1991; Meijer et al., 2021).

 

Figure 4: Variability in location quotients: Distribution by standard deviation (10,000 geocoordinates, quartiled)

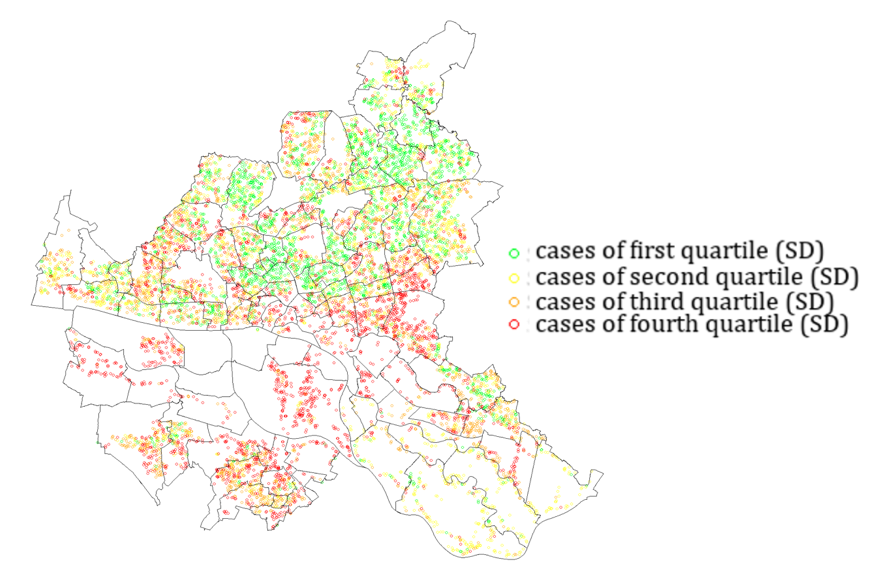
A low standard deviation (1st quartile) across 10 operationalizations of areal units suggests a stable proportional distribution of Germans and foreigners, implying consistent spatial patterns. Moreover, the location quotient and its standard deviation (SD) rarely exceed 1, indicating substantial consistency and a potentially trivial impact of MAUP. This stability is observed in areas characterized by relatively homogeneous spatial distributions of foreigners and Germans. In contrast, cases with high standard deviations (4th quartile) are situated in regions exhibiting heterogeneous distributions of characteristics, where spatial rescaling substantially affects the location quotient. Figure 5 illustrates distinct clusters of geocoordinates with high and low standard deviations, visualizing the divergent patterns of homogeneous and heterogeneous distributions. Notably, the reference spatial unit remains consistent throughout the analysis.

 

Figure 5: Quartile distribution of standard deviation (SD): Spatial patterns of homogeneity and heterogeneity

These findings offer a partial explanation for the divergent perspectives on the relevance of MAUP, as evident in the disparate views presented by Reardon and O’Sullivan (2004) and Wooldredge (2002). The divergent views can be attributed to the utilization of distinct data sources, often derived from different regional contexts, which underscores the context-dependent nature of MAUP’s relevance. Consequently, the comparability of results across studies is compromised, as the use of varying spatial scales, zoning systems, and data sources can lead to inconsistent measurements and interpretations of segregation patterns. This lack of comparability hinders the ability to generalize findings and draw meaningful conclusions about the dynamics of segregation across different regions and contexts.

Conclusion

The sensitivity of segregation metrics to variations in spatial operationalization appears to be contingent upon the underlying distribution of socio-spatial characteristics across geographic space, a phenomenon that often remains opaque or can only be approximated. I propose a hypothesis: assuming a relatively uniform distribution of the characteristics of interest across space, MAUP should have a limited impact on local and global segregation estimates and correlations. In contrast, when the distribution of characteristics is heterogeneous, neglecting to account for MAUP can lead to significant distortions in segregation metrics. A comparative analysis of segregation patterns in Munich, characterized by relatively low ethnic-segregation (Meister & Niebuhr, 2020), permits an examination of this hypothesis.

The findings reveal a robust correlation between German and foreign populations across 10 spatial operationalizations (average correlation: Hamburg = 0.7, Munich = 0.8), indicating a consistent distribution pattern. Notably, global segregation measurements exhibit higher consistency across operationalizations in Munich than in Hamburg, as evidenced by the mean and SD of the spatial dissimilarity index (HH: 0.16 ± 0.015, M: 0.12 ± 0.013).

Moreover, the analysis of local segregation patterns, as captured by the location quotient, reveals reduced variability in estimates across the 10 measurements, with lower standard deviations observed in Munich (Q1 = 0.10, Q2 = 0.15, Q3 = 0.21, Q4 = 0.35) than in Hamburg (Q1 = 0.12, Q2 = 0.18, Q3 = 0.25, Q4 = 0.51) across all four quartiles, indicating more consistent and robust estimates. Despite the overall low level of segregation in Munich reflected in the low values of the location quotient at the local level, a substantial proportion (40.11%) of inconsistencies emerge in the substantive interpretation of the location quotient, highlighting the complexities of segregation dynamics at the local level. To further evaluate the reliability of local segregation estimates, I employed the intraclass correlation coefficient (ICC), a statistical measure that captures both the degree of correlation and agreement between measurements (Koo & Li, 2016). The ICC values for Hamburg and Munich reveal poor reliability, with ICC(A,1) = 0.62 for Hamburg and ICC(A,1) = 0.55 for Munich, indicating poor test–retest reliability and consistency for both cities. Notably, the ICC value for Munich fell short of expectations, suggesting that the reliability of local segregation estimates in Munich is less robust than anticipated. The initial hypothesis can only be partially accepted, as it holds true for global segregation measures but not local segregation values. These preliminary findings suggest that approximating the potential impact of MAUP in the absence of adequate spatial data by calculating relatively MAUP-robust estimators, as demonstrated by Meister and Niebuhr (2020), may not be a viable solution. However, a more rigorous and systematic examination of this concept could potentially uncover untapped opportunities for improving segregation metrics.

In the context of calculating segregation at the local level, the simplistic notion that ‘smaller is always better’ does not hold true (Oberwittler & Wikström, 2009). As illustrated in Figure 4 (1st quartile), the substantive interpretation of the coefficients remains largely unaffected or only slightly biased, even when employing fairly large areal units. However, it would be misguided to argue that aggregation is inconsequential (Wooldredge, 2002), as the substantive interpretation of the results can change significantly in cases with high standard deviations (4th quartile, Figure 4). Thus, the pursuit of a technical, one-size-fits-all solution to MAUP appears futile.

Instead, the focus must shift to the theoretical underpinnings of the shape, form, and size of the spatial unit of interest. MAUP is a phenomenon that requires theoretically informed decisions regarding the spatial scale of analysis and the reference units, rather than a problem that can be addressed through technical solutions (Andresen, 2021; Fotheringham & Wong, 1991; Openshaw & Taylor, 1979; Wong, 2004, 2009). Theoretical justification is paramount when selecting or generating scales or zones of areal units in segregation research (Hipp, 2007). Unfortunately, atheoretical scalings and zonings persist, often driven by data availability rather than theoretical foundations. As data availability continues to improve, it is essential to theoretically justify the choice of zonings and scales, which necessitates an understanding of the underlying mechanisms of action. For instance, a school tract may be a suitable unit for analyzing the impact of segregation on school children, whereas ego-centred or activity space (Li et al., 2022) operationalizations are necessary when examining social interactional mechanisms (Galster, 2012). A thorough understanding of the theorized data-generating process enables a theory-driven selection or generation of spatial areal units and reference spatial units, as well as an assessment of the appropriateness of the employed spatial layout. Consequently, the pursuit of optimal zoning or natural zoning is crucial, as it aims to identify areal units that possess inherent relevance (Openshaw, 1984).

MAUP undermines a fundamental principle of comparative research – namely, the ability to draw inferences about mechanisms by comparing different outcomes under comparable or controlled situations. Specifically, MAUP threatens the comparability of conditions under which a certain outcome is observed, rendering inferences based on such comparisons problematic or susceptible to error, as previously illustrated. Consequently, theoretically sound operationalizations of socio-spatial units, despite varying in shape and size, would yield comparable results, enabling meaningful comparisons and inferences across different contexts. This, in turn, would facilitate a more nuanced understanding of the relationships between socio-spatial units and the phenomena being studied, ultimately leading to more robust and generalizable findings.

The primary conclusion of this research note is that segregation metrics, such as the adjusted spatial dissimilarity index (Lee et al., 2008, p. 769), have the potential to serve as a proxy indicator for evaluating the potential severity of MAUP in both global and local segregation analyses, provided that they are employed with caution and consideration. However, it is crucial to emphasize that a theoretically grounded approach, such as the implementation of optimal zoning strategies, should be prioritized over technical approaches that may overlook the complexities of socio-spatial relationships. The latter approach is particularly important, as it acknowledges the inherent complexities of spatial data and the need for a nuanced understanding of the relationships between socio-spatial units and the phenomena being studied. By adopting a theoretically informed approach, researchers can ensure that their analyses are grounded in a robust understanding of the spatial context, which enhances the accuracy and reliability of comparisons across different settings. Ultimately, this enables the development of more comprehensive and generalizable findings that can inform policy and practice in a meaningful way.

References

1. Amrhein, C. G. (1995). Searching for the Elusive Aggregation Effect: Evidence from Statistical Simulations. Environment and Planning A, 27(1), 105–119. https://doi.org/10.1068/a270105
2. Andersson, E. K., Lyngstad, T. H., & Sleutjes, B. (2018). Comparing Patterns of Segregation in North-Western Europe: A Multiscalar Approach. European Journal of Population, 34(2), 151–168. https://doi.org/10.1007/s10680-018-9477-1
3. Andresen, M. A. (2021). Modifiable Areal Unit Problem. In The Encyclopedia of Research Methods in Criminology and Criminal Justice (pp. 854–855). John Wiley & Sons, Ltd. https://doi.org/10.1002/9781119111931.ch164
4. Arribas-Bel, D., Nijkamp, P., & Poot, J. (2016). How diverse can measures of segregation be? Results from Monte Carlo simulations of an agent-based model. Environment and Planning A: Economy and Space, 48(10), 2046–2066. https://doi.org/10.1177/0308518X16653402
5. BKG. (2017). Dokumentation Geographische Gitter für Deutschland GeoGitter. Bundesamt für Kartographie und Geodäsie. https://sg.geodatenzentrum.de/web_public/gdz/dokumentation/deu/geogitter.pdf
6. Bömermann, H. (2011). Leben Berliner mit Migrationshintergrund segregiert? Zeitschrift für amtliche Statistik Berlin Brandenburg, 3, 54–73.
7. Clark, W., & Avery, K. (1976). The Effect of Data Aggregation in Statistical Analysis. Geographical Analysis, 8(4), 428–438. https://doi.org/10.1111/j.1538-4632.1976.tb00549.x
8. Costa, R., & De Valk, H. A. G. (2018). Ethnic and Socioeconomic Segregation in Belgium: A Multiscalar Approach Using Individualised Neighbourhoods. European Journal of Population, 34(2), 225–250. https://doi.org/10.1007/s10680-018-9480-6
9. Destatis. (2018). Zensus 2011 Haushalte je Hektar. Ergebnisse des Zensus am 9. Mai 2011 in Gitterzellen. https://www.zensus2011.de/DE/Home/Aktuelles/DemografischeGrunddaten.html
10. Duncan, O. D., & Duncan, B. (1955). A Methodological Analysis of Segregation Indexes. American Sociological Review, 20(2), 210–217. https://doi.org/10.2307/2088328
11. Engstrom, E. J. (2013). Partisan Gerrymandering and the Construction of American Democracy. University of Michigan Press. https://doi.org/10.2307/j.ctt1gk086k
12. Fotheringham, A., Stewart, & Wong, D., W. S. (1991). The Modifiable Areal Unit Problem in Multivariate Statistical Analysis. Environment and Planning A: Economy and Space, 23(7), 1025–1044. https://doi.org/10.1068/a231025
13. Galster, G. C. (2012). The Mechanism(s) of Neighbourhood Effects: Theory, Evidence, and Policy Implications. In M. Van Ham, D. Manley, N. Bailey, L. Simpson, & D. Maclennan (Eds.), Neighbourhood Effects Research: New Perspectives (pp. 23–56). Springer VS.
14. Getis, A., & Ord, J. K. (2010). The Analysis of Spatial Association by Use of Distance Statistics. Geographical Analysis, 24(3), 189–206. https://doi.org/10.1111/j.1538-4632.1992.tb00261.x
15. Hennerdal, P., & Nielsen, M. M. (2017). A Multiscalar Approach for Identifying Clusters and Segregation Patterns That Avoids the Modifiable Areal Unit Problem. Annals of the American Association of Geographers, 107(3), 555–574. https://doi.org/10.1080/24694452.2016.1261685
16. Hipp, J. R. (2007). Block, Tract, and Levels of Aggregation: Neighborhood Structure and Crime and Disorder as a Case in Point. American Sociological Review, 72(5), 659–680. https://doi.org/10.1177/000312240707200501
17. Hong, S.-Y., O’Sullivan, D., & Sadahiro, Y. (2014). Implementing Spatial Segregation Measures in R. PLoS ONE, 9(11), e113767. https://doi.org/10.1371/journal.pone.0113767
18. Koo, T. K., & Li, M. Y. (2016). A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. Journal of Chiropractic Medicine, 15(2), 155–163. https://doi.org/10.1016/j.jcm.2016.02.012
19. Lee, B. A., Reardon, S. F., Firebaugh, G., Farrell, C. R., Matthews, S. A., & O’Sullivan, D. (2008). Beyond the Census Tract: Patterns and Determinants of Racial Segregation at Multiple Geographic Scales. American Sociological Review, 73(5), 766–791. https://doi.org/10.1177/000312240807300504
20. LGV. (2016). ALKIS Verwaltungsgrenzen Hamburg [GML]. https://daten-hamburg.de/geographie_geologie_geobasisdaten/ALKIS_Verwaltungsgrenzen/ALKISVerwaltungsgrenzen_HH_2016-03-07.zip
21. Li, Q.-Q., Yue, Y., Gao, Q.-L., Zhong, C., & Barros, J. (2022). Towards a new paradigm for segregation measurement in an age of big data. Urban Informatics, 1(1), 5. https://doi.org/10.1007/s44212-022-00003-3
22. Lichter, D. T., Parisi, D., & Taquino, M. C. (2015). Toward a New Macro-Segregation? Decomposing Segregation within and between Metropolitan Cities and Suburbs. American Sociological Review, 80(4), 843–873. https://doi.org/10.1177/0003122415588558
23. Meijer, E., Oczkowski, E., & Wansbeek, T. (2021). How measurement error affects inference in linear regression. Empirical Economics, 60(1), 131–155. https://doi.org/10.1007/s00181-020-01942-z
24. Meister, M., & Niebuhr, A. (2020). Comparing ethnic segregation across cities—Measurement issues matter. Review of Regional Research, 41(1), 33–54. https://doi.org/10.1007/s10037-020-00145-4
25. Oberwittler, D., & Wikström, P.-O. H. (2009). Why Small Is Better: Advancing the Study of the Role of Behavioral Contexts in Crime Causation. In D. Weisburd, W. Bernasco, & G. J. N. Bruinsma (Eds.), Putting Crime in its Place: Units of Analysis in Geographic Criminology (pp. 35–59). Springer. https://doi.org/10.1007/978-0-387-09688-9_2
26. Openshaw, S., Peter. (1984). The Modifiable Areal Unit Problem. Concepts and Techniques in Modern Geography Number, 38.
27. Openshaw, S., Peter, & Taylor, J. (1979). A million or so correlation coefficients: Three experiments on the modifiable area unit problem. In N. Wrigley (Ed.), Statistical Applications in the Spatial Sciences (pp. 127–144).
28. Reardon, S. F., & O’Sullivan, D. (2004). Measures of Spatial Segregation. Sociological Methodology, 34(1), 121–162. https://doi.org/10.1111/j.0081-1750.2004.00150.x
29. Tobler, W. R. (1970). A Computer Movie Simulating Urban Growth in the Detroit Region. Economic Geography, 46, 234. https://doi.org/10.2307/143141
30. Wong, D., W. S. (2004). The Modifiable Areal Unit Problem (MAUP). In D. G. Janelle, B. Warf, & K. Hansen (Eds.), WorldMinds: Geographical Perspectives on 100 Problems (pp. 571–575). Springer.
31. Wong, D., W. S. (2009). Modifiable Areal Unit Problem. In R. Kitchin & N. Thrift (Eds.), International Encyclopedia of Human Geography (pp. 169–174). Elsevier. https://doi.org/10.1016/B978-008044910-4.00475-2
32. Wooldredge, J. (2002). Examining the (IR) Relevance of Aggregation Bias for Multilevel Studies of Neighborhoods and Crime with an Example Comparing Census Tracts to Official Neighborhoods in Cincinnati. 40(3), 681–709.