Inferences based on Probability Sampling or Nonprobability Sampling – Are They Nothing but a Question of Models?
Quatember A. (2019), Inferences based on Probability Sampling or Nonprobability Sampling – Are They Nothing but a Question of Models? Survey Methods: Insights from the Field. Retrieved from https://surveyinsights.org/?p=11203
© the authors 2019. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0) 
Abstract
The inferential quality of an available data set, be it from a probability sample or a nonprobability sample, is discussed under the standard of the representativeness of a sample with regard to interesting characteristics, which implicitly includes the consideration of the total survey error. The paper focuses on the assumptions that are made when calculating an estimator of a certain population characteristic using a specific sampling method, and on the model-based repair methods, which can be applied in the case of deviations from these assumptions. The different implicit assumptions regarding operationalization, frame, selection method, nonresponse, measurement, and data processing are considered exemplarily for the Horvitz-Thompson estimator of a population total. In particular, the remarkable effect of a deviation from the assumption concerning the selection method is discussed. It is shown that there are far more unverifiable, disputable models addressing the different implicit assumptions needed in the nonprobability approach to sampling, including big data. Moreover, the definition of the informative samples with respect to the expressed survey purpose is presented, which complements the definition of the representativeness of samples in the practice of survey sampling. Finally, an answer to the question in the title of this study is given and detailed reports regarding the applied survey design are recommended.
Keywords
Representativeness, Sample surveys, Sampling techniques, Survey methodology, total survey error
Copyright
© the authors 2019. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0) 
Introduction
There is a constantly increasing demand for objective information about some characteristics of finite populations of interest based on data. Regarding the sources of such data, in this paper, we will distinguish between probability samples and nonprobability samples.
The probability sampling techniques can be described under a unique theoretical framework because they all share the fact that they assign a known, nonzero sample selection probability to each unit of the target population (cf., for instance, the textbooks by Särndal et al. 1992, or Lohr 2010). Examples of such sampling schemes include simple, stratified, cluster, multistage, or probability proportional to size random sampling. The essential aspect of these procedures is that the known selection probabilities of the sample members allow a design-unbiased point estimation of population characteristics, such as totals, means, or proportions. However, for example, non-negligible nonresponse rates may require the formulation of models regarding the mechanism that generates such a behavior.
In contrast to the probability sampling schemes, the different nonprobability sampling techniques have only little more in common than the lack of knowledge of the associated selection probabilities. Therefore, in contrast to the probability sampling schemes, to be able to conduct inferential statistics, these methods will also require model assumptions to explain the selection process itself. Examples of such techniques are the purposive methods of quota or expert choice sampling; the link-tracing designs, such as snowball or respondent-driven sampling that are particularly used with hard-to-reach populations (cf., for instance, Tourangeau et al. 2014); and the arbitrary sampling methods, such as volunteer or river sampling.
In the context of this paper, the term “big data” will refer to big, not survey-, but process-generated, hence, non-probabilistic data sets, which primarily were not collected with the intention to conclude on population characteristics. Examples of such process-generated data collections are those collected by mobile phones’ network providers, which are used to estimate temporal variations in population density, social media data used to estimate flows in the labor market, or crime-related data, which are analyzed in the field of crime prediction.
For the purpose of setting the standard regarding the quality of sample results, the term“representativeness”, which has been used in so many different meanings (cf. Kruskal and Mosteller 1980), is defined as the indicator of the inference quality of survey outcomes (cf. Quatember 2019):
A sample is called “representative” with respect to a certain population characteristic (such as a whole distribution of a study variable or a parameter of this distribution) if this characteristic can be (at least approximately) unbiasedly estimated from the available data with a predefined accuracy.
In this definition, the goal of representativeness of a sample is described by the statistical similarity concept of the unbiasedness of estimators (cf. Särndal et al. 1992, 40) and by a requirement regarding the efficiency of the estimates. Hence, it implicitly includes the consideration of the total survey error– a concept that addresses both the sampling error, which describes the sample-to-sample variation of estimators, and the systematic (or nonsampling) error that can also occur in population surveys (cf. Weisberg 2005). In the context of statistical surveys, the term “error” refers to the difference between an estimate of a population characteristic and its true value. Several types of errors, in particular the frame error, the nonresponse error, the measurement error, and the processing error contribute to the nonsampling error.
In the subsequent section, the different implicit assumptions that are made when a specific estimator of a population characteristic is applied to any sampling method, are discussed exemplarily for the expression of the Horvitz-Thompson estimator of a population total under simple random sampling without replacement. In particular, the remarkable effect of a deviation from the assumption concerning the selection method is presented. Furthermore, the statistical repair methods that may reduce the increase of the total survey error caused by deviations from these implicitly made assumptions are considered. Complementing the definition of the representative samples from above, the definition of the informative samples with regard to the declared survey purpose, which may prove useful in practice, is presented in Section 3. In the concluding section, the question asked in the title of the paper is discussed again and answered.
Implicit assumptions and explicit models
Let the task be the estimation of a certain population characteristic from the finite target population ![]() of size
of size ![]() . Throughout the paper, as it is quite common in textbooks in the field of sampling theory (cf., for instance, Särndal et al. 1992), let the population total
. Throughout the paper, as it is quite common in textbooks in the field of sampling theory (cf., for instance, Särndal et al. 1992), let the population total
(1) ![]()
(![]() denotes the sum over all units of
denotes the sum over all units of ![]() ) of a variable
) of a variable ![]() under study serve as the example of a population characteristic of interest in
under study serve as the example of a population characteristic of interest in ![]() . Therein,
. Therein, ![]() denotes the fixed
denotes the fixed ![]() -value of population unit
-value of population unit ![]() .
.
Under the laboratory conditions of the urn model from probability theory, in a probability sample ![]() of size
of size ![]() (
(![]() ,
, ![]() ), drawn according to some probability sampling scheme
), drawn according to some probability sampling scheme ![]() with known sample selection probabilities, the Horvitz-Thompson estimator
with known sample selection probabilities, the Horvitz-Thompson estimator
(2) ![]()
is design-unbiased for ![]() with variance
with variance ![]() (cf., for instance, Särndal et al. 1992, 42-48). In (2), the
(cf., for instance, Särndal et al. 1992, 42-48). In (2), the ![]() denotes the design weights of the sample elements that are defined as the reciprocals of the sample selection probabilities.
denotes the design weights of the sample elements that are defined as the reciprocals of the sample selection probabilities.
Therefore, for simple random sampling without replacement (SI) with the probabilities ![]() of being selected for the SI sample
of being selected for the SI sample ![]() , the Horvitz-Thompson estimator (2) is given by
, the Horvitz-Thompson estimator (2) is given by
(3) ![]()
which results in ![]() times the sample mean of
times the sample mean of ![]() , with variance
, with variance ![]() .
.
However, what about using, for instance, this estimator under real conditions? Another question is, what about using expression (3) for nonprobability samples, for which an estimator also has to be calculated although the selection probabilities are unknowable?
Formally, the application of (3) to an available data set ![]() , be it a probability or a nonprobability sample drawn by a sampling method
, be it a probability or a nonprobability sample drawn by a sampling method ![]() , results in
, results in
(4) ![]()
which only for an SI sample (with ![]() ) provides the estimator (3) with its known statistical properties. The usage of this estimator is based on several assumptions that are discussed in the following together with the models that have to be applied in the case of deviations from these assumptions:
) provides the estimator (3) with its known statistical properties. The usage of this estimator is based on several assumptions that are discussed in the following together with the models that have to be applied in the case of deviations from these assumptions:
The operationalization assumption: The first implicit assumption when an estimator such as (4) is applied to an available data set ![]() collected by a probability or a nonprobability sampling method
collected by a probability or a nonprobability sampling method ![]() , is that variable
, is that variable ![]() actually measures what is intended to be measured. In other words, it is assumed that the research questions are correctly operationalized. In the big data context of nonprobability sampling, this assumption plays a special role because there the research topics usually have to orient themselves on the available data sets and not the other way around as it is usual in empirical research. An example is the Google project on flu trends, in which records of search entries were analyzed to find those flu-related terms that can be used for the estimation of flu prevalence. However, after an initial success, together with a media-stoked increase of relevant searches, Google’s constantly tested and improved auto-suggest feature and other changes in the search algorithms led to a persistent overestimation of the flu prevalence because these search items lost their predictive value (cf., for instance, Lazer et al. 2014, 1203).
actually measures what is intended to be measured. In other words, it is assumed that the research questions are correctly operationalized. In the big data context of nonprobability sampling, this assumption plays a special role because there the research topics usually have to orient themselves on the available data sets and not the other way around as it is usual in empirical research. An example is the Google project on flu trends, in which records of search entries were analyzed to find those flu-related terms that can be used for the estimation of flu prevalence. However, after an initial success, together with a media-stoked increase of relevant searches, Google’s constantly tested and improved auto-suggest feature and other changes in the search algorithms led to a persistent overestimation of the flu prevalence because these search items lost their predictive value (cf., for instance, Lazer et al. 2014, 1203).
The frame assumption: The next implicit assumption, when the estimator (4) is applied in the practice of survey sampling, is that the available sampling frame ![]() , from which the members of the sample
, from which the members of the sample ![]() are actually recruited by the sampling method
are actually recruited by the sampling method ![]() , corresponds to the real study population
, corresponds to the real study population ![]() , or that
, or that ![]() and
and ![]() only differ negligibly with respect to the interesting characteristic. In other words, it is either assumed that there is no frame error or that there is an ignorable coverage bias, which is defined as the difference of the expected value of the estimator
only differ negligibly with respect to the interesting characteristic. In other words, it is either assumed that there is no frame error or that there is an ignorable coverage bias, which is defined as the difference of the expected value of the estimator ![]() of the total of
of the total of ![]() in
in ![]() and the total
and the total ![]() in
in ![]() , so that
, so that ![]() is representative with respect to the population total, when no other nonsampling errors apply. For nonprobability sampling schemes, the avoidance of a non-ignorable coverage bias is the big challenge because the frame population of potential sample members almost always excludes very large parts of the target population from the possible sample membership.
is representative with respect to the population total, when no other nonsampling errors apply. For nonprobability sampling schemes, the avoidance of a non-ignorable coverage bias is the big challenge because the frame population of potential sample members almost always excludes very large parts of the target population from the possible sample membership.
With covariates available in ![]() and
and ![]() , this assumption can be tested. After that, an expected non-ignorable coverage bias can be reduced by an explicitly formulated model concerning the distributions of the interesting variable
, this assumption can be tested. After that, an expected non-ignorable coverage bias can be reduced by an explicitly formulated model concerning the distributions of the interesting variable ![]() and these auxiliary variables, for instance, in a ratio estimation approach (cf., for instance, Särndal et al. 1992, 540-546).
and these auxiliary variables, for instance, in a ratio estimation approach (cf., for instance, Särndal et al. 1992, 540-546).
The sample selection assumption: A third assumption that is implicitly made when the estimator
![]()
is applied to an available sample ![]() , is that the used sampling technique
, is that the used sampling technique ![]() actually provides the SI selection probabilities that are used for the calculation of the design weights
actually provides the SI selection probabilities that are used for the calculation of the design weights ![]() in (4). In other words, it is either assumed that there is no selection error with regard to the presumed selection probabilities or that there is no selection bias resulting from that error.
in (4). In other words, it is either assumed that there is no selection error with regard to the presumed selection probabilities or that there is no selection bias resulting from that error.
For an insight into the impact of such a bias, estimator (4) is rewritten by
![]()
with the sample membership indicator ![]() of population unit
of population unit ![]() and the deviation
and the deviation ![]() of the unit’s
of the unit’s ![]() -value from the population mean
-value from the population mean ![]() (cf. Ardilly and Tillé 2006, 111-114, Meng 2018, 689-700). With
(cf. Ardilly and Tillé 2006, 111-114, Meng 2018, 689-700). With ![]() , the population sum
, the population sum ![]() of the products of the sample membership indicators
of the products of the sample membership indicators ![]() (with population mean
(with population mean ![]() ) and the
) and the ![]() -values can be written as
-values can be written as
![]()
with the “(![]() )-population covariance”
)-population covariance”
![]()
of ![]() and
and ![]() (cf., for instance, Särndal et al. 1992, 186). The population correlation
(cf., for instance, Särndal et al. 1992, 186). The population correlation ![]() of these variables under sampling technique
of these variables under sampling technique ![]() is given by
is given by
![]()
with ![]() and
and ![]() , the “(
, the “(![]() )-population variances” of
)-population variances” of ![]() and
and ![]() , respectively. Moreover,
, respectively. Moreover, ![]() applies (cf., for instance, Särndal et al. 1992, 36). Hence, the actual estimation error
applies (cf., for instance, Särndal et al. 1992, 36). Hence, the actual estimation error ![]() of the estimate
of the estimate ![]() is given by
is given by
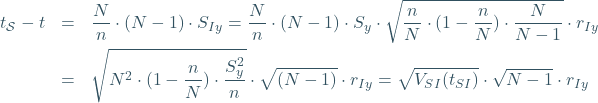
with ![]() , the variance of
, the variance of ![]() under SI sampling. Since the biased estimation shall be addressed, Meng (2018) defines the design effect
under SI sampling. Since the biased estimation shall be addressed, Meng (2018) defines the design effect ![]() as the ratio of the mean square errors
as the ratio of the mean square errors ![]() of the applied estimator
of the applied estimator ![]() under the sampling method
under the sampling method ![]() that was actually used and
that was actually used and ![]() under SI sampling (cf., ibid., 696). This is derived from
under SI sampling (cf., ibid., 696). This is derived from
(5) ![Rendered by QuickLaTeX.com \begin{eqnarray*} MSE_{\mathcal{S}}(t_{\mathcal{S}})&=&E_{\mathcal{S}}[(t_{\mathcal{S}}-t)^2]=E_{\mathcal{S}}[V_{SI}(t_{SI})\cdot (N-1)\cdot r_{Iy}^2]\notag \\&=&V_{SI}(t_{SI})\cdot \underbrace{(N-1)\cdot E_{\mathcal{S}}(r_{Iy}^2)}_{\equiv D_{\mathcal{S}}} \end{eqnarray*}](https://surveyinsights.org/wp-content/uploads/ql-cache/quicklatex.com-abf90d28d6b8fd7a5ad93ad23365110d_l3.png)
In the design effect ![]() , the second term on the right-hand side is a measure of the selection bias when using the estimator
, the second term on the right-hand side is a measure of the selection bias when using the estimator ![]() for the data collected by a technique
for the data collected by a technique ![]() . Obviously, for SI sampling,
. Obviously, for SI sampling, ![]() applies. For any other method
applies. For any other method ![]() , for which
, for which ![]() applies, the usage of the usual SI variance estimation formula under the sampling method
applies, the usage of the usual SI variance estimation formula under the sampling method ![]() that was actually applied leads to the following two negative effects (cf. Meng 2018, 700-701):
that was actually applied leads to the following two negative effects (cf. Meng 2018, 700-701):
- The actual coverage rates of the common approximate confidence intervals are too small;
- The true significance levels for hypotheses tests are too large, thus resulting in too many significant results under the null hypothesis.
The essence of (5) is that for a given population size ![]() the design effect
the design effect ![]() does not depend on the size
does not depend on the size ![]() of the sample at all because
of the sample at all because ![]() only influences the term
only influences the term ![]() . In other words,
. In other words, ![]() does not depend on how“big” the data is, but only on the deviation of the true sample selection probabilities of the sampling technique
does not depend on how“big” the data is, but only on the deviation of the true sample selection probabilities of the sampling technique ![]() that was actually applied from the SI selection probabilities applied in (4). For
that was actually applied from the SI selection probabilities applied in (4). For ![]() , the bias of
, the bias of ![]() takes over the leading role in the mean square error
takes over the leading role in the mean square error ![]() . If
. If ![]() is large, a tiny deviation of the true selection mechanism from the implicit SI assumption already results in a large design effect
is large, a tiny deviation of the true selection mechanism from the implicit SI assumption already results in a large design effect ![]() with a devastating impact on the estimator’s inferential quality.
with a devastating impact on the estimator’s inferential quality.
This may apply to complex probability sampling, when for the sake of simplicity, this selection model is used in the statistical analysis although the true design weights are knowable (cf. Bacher 2009). For nonprobability sampling, the validity of this sample selection model, which is applied in many settings, will almost always be in doubt, yielding the described consequences. As an alternative approach to such a naïve explicit modeling of the unknown sample selection probabilities of nonprobability sampling, estimates of these probabilities can be used for the calculation of the design weights needed in (2). This estimation relies on auxiliary variables (such as demographic characteristics) that on the one hand should explain the unknown nonprobability sample selection probabilities and on the other hand are available for the given nonprobability sample as well as for a probability sample or the population (cf., for instance, Elliot 2009).
Statistical methods such as poststratification or iterative proportional fitting can be applied. Such methods match the sample to given population distributions of available auxiliary variables with the aim of reducing selection bias by adjusting the modeled design-weights (cf., for instance, Lohr 2010, 340-346).
The nonresponse assumption: Another implicit assumption of the application of the estimator (4) is that all elements in the drawn sample ![]() are available and willing to respond. In other words, it is assumed that there is no nonresponse (even in surveys on sensitive topics or in hard-to-reach and hard-to-ask populations) or, if this is not the case, at least only a negligible nonresponse bias exists.
are available and willing to respond. In other words, it is assumed that there is no nonresponse (even in surveys on sensitive topics or in hard-to-reach and hard-to-ask populations) or, if this is not the case, at least only a negligible nonresponse bias exists.
When despite all efforts to prevent high nonresponse rates given the applied survey mode, nonresponse occurs, according to (5), the design effect ![]() of the sampling technique
of the sampling technique ![]() that was actually applied will be affected by an increase of the expected value
that was actually applied will be affected by an increase of the expected value ![]() , where variable
, where variable ![]() now indicates the sample membership of the responding units. A measure of this impact of nonresponse on the inference quality is given by the representativeness-indicator (Schouten et al. 2009). This measure is a function of the variance of response probabilities in
now indicates the sample membership of the responding units. A measure of this impact of nonresponse on the inference quality is given by the representativeness-indicator (Schouten et al. 2009). This measure is a function of the variance of response probabilities in ![]() . The larger this variance, the lower is the representativeness of the given responses. In this way, the representativeness-indicator estimates the deviation of the actual nonresponse mechanism from being completely at random and thus, the potential for a non-ignorable nonresponse bias.
. The larger this variance, the lower is the representativeness of the given responses. In this way, the representativeness-indicator estimates the deviation of the actual nonresponse mechanism from being completely at random and thus, the potential for a non-ignorable nonresponse bias.
The complete ignorance of nonresponse in the estimation process is a common practice, which means that the nonresponse that occurred is modeled as being completely at random (cf., for instance, Little and Rubin 2002, 12). In particular, in the application of the nonprobability sampling methods, a nonrespondent is usually simply replaced by the next suitable person who is willing to cooperate and nonresponse rates are usually not reported for the resulting data sets.
However, in the presence of non-ignorable nonresponse, it is impossible to calculate reliable estimates of population characteristics of interest, such as the total ![]() by a formula like (4) without any intervention in the estimation process. For this purpose, for example, the statistical repair methods of weighting adjustment to compensate for the unit-nonresponse that occurred (by procedures such as poststratification or iterative proportional fitting) and data imputation for the item-nonresponse (by techniques, such as mean or regression imputation) can be applied to reduce the amount of the nonresponse bias under adequate and explicitly formulated models regarding the nonresponse mechanism (cf., for instance, Bethlehem et al. 2011, Chaps. 8 and 14).
by a formula like (4) without any intervention in the estimation process. For this purpose, for example, the statistical repair methods of weighting adjustment to compensate for the unit-nonresponse that occurred (by procedures such as poststratification or iterative proportional fitting) and data imputation for the item-nonresponse (by techniques, such as mean or regression imputation) can be applied to reduce the amount of the nonresponse bias under adequate and explicitly formulated models regarding the nonresponse mechanism (cf., for instance, Bethlehem et al. 2011, Chaps. 8 and 14).
The measurement and data processing assumption: With the application of an estimator such as
![]()
it is further assumed that there are no untruthful answers given or wrong measurements as well as no processing errors, such as a data encoding error. If this does not apply, it is at least assumed that there is no non-negligible measurement and data processing bias, respectively.
To reduce the extent of an occurred measurement or data processing error, an explicitly formulated plausible stochastic model describing the mechanisms that led to the wrong observations can be applied to calculate a reliable estimate (cf. for instance, Särndal et al. 1992, 601-634).
The task force of the Executive Council of the American Association of Public Opinion Research (AAPOR) had the task “o examine the condition under which various survey designs that do not use probability samples might still be useful for making inferences to a larger population (cf. Baker et al. 2013, 6).” It was noted that the different nonprobability sampling techniques can be thought of “as falling on a continuum of expected accuracy of the estimates (ibid., 105).” At one end of the quality scale, are the completely uncontrolled arbitrary samples, whereas at the other end, are the methods based on less risky selection procedures in which the results are adjusted as described above, using auxiliary variables that are correlated with the variables of interest (cf. Baker et al. 2013, 105-106).
A complementary concept on the inferential quality of surveys
Suggesting the definition of representativeness in Section 1, in the practice of sampling, it cannot be ignored that it is often sufficient to get a very rough idea of a population characteristic of interest. Examples from empirical sciences include pretests or pilot studies, but there are also public surveys, for instance, to identify some of the causes of a possible dissatisfaction among community residents that fall into this category of surveys. When nothing or very little is known about characteristics of interest describing, for instance, a hard-to-reach population, the following supplementary definition takes account of this fact (Quatember 2001, 20):
A sample is called “informative” for a certain population characteristic if it provides sufficient information on that characteristic with respect to the declared survey purpose.
Herein, the acceptable degree of inaccuracy is mainly determined by the usefulness of the resulting outcomes with respect to the purpose of the survey, which does not always have to be a high-quality inference from a representative sample to the target population.
Conclusions
The question was this: Inferences based on probability sampling or nonprobability sampling – are they nothing but a question of models? The answer is this: Yes, they are!– but only under certain implicit assumptions and explicit models to react on deviations, in this regard as discussed in Section 2 exemplarily for the usage of the Horvitz-Thompson estimator (3) of SI sampling for a total (1) of a variable under study. It is implicitly assumed that there is no operationalization, coverage, selection, nonresponse, measurement, or processing bias. In the presence of deviations from these basic assumptions, facing the risk of a substantially biased estimator, a model-based estimation has to be established instead. For this purpose, complementary explicit models have to be formulated concerning these deviations between theory and practice. Then, even the representativeness of a probability sample is only valid under these models, which always applies to nonprobability samples.
However, is there a difference between probability samples and nonprobability samples regarding these models? Again, the answer is: Yes! There are far more unverifiable, disputable models that address the different implicit assumptions, needed in the nonprobability approach to sampling, including big data. Nevertheless, the application of a nonprobability sampling technique instead of a probability sampling method might be justified for specific research objectives concerning, for example, special populations, such as hard-to-reach ones, for which informative instead of representative samples, according to the additionally presented definition in Section 3, are sufficient. However, if high-quality inference is the survey purpose, it is still the theory of probability sampling that sets the standard and serves as a landmark.
As a consequence of the different strengths of model-dependencies and the varying intended research purposes, sufficient details about the applied sampling design and the survey purpose shall have to be standardly reported along with all the applied implicit assumptions and explicit models. Only such a report may enable data users to assess the real quality of produced survey results.
References
- Ardilly, P, and Tillé, Y. (2006). Sampling Methods. Exercises and Solutions. New York: Springer.
- Bacher, J. (2009). Analyse komplexer Stichproben. In: Weichbold, M., Bacher, J., and Wolf, C. (eds.). Umfrageforschung. Herausforderungen und Grenzen. Österreichische Zeitschrift für Soziologie. Vierteljahresschrift der Österreichischen Gesellschaft für Soziologie. 34. Jahrgang, Sonderheft 9. Wiesbaden: VS Verlag für Sozialwissenschaften. [in German]
- Baker, R., Brick, J.M., Bates, N.A., Battaglia, M., Couper, M.P., Dever, J.A., Gile, K.J., and Tourangeau, R. (2013). Report of the AAPOR Task Force on Non-probability Sampling. https://www.aapor.org/AAPOR_Main/media/MainSiteFiles/NPS_TF_Report_Final_7_revised_FNL_6_22_13.pdf (assessed on 08-07-2018)
- Bethlehem, J., Cobben, F., and Schouten, B. (2011). Handbook of Nonresponse in Household Surveys. Hoboken: Wiley.
- Elliott, M.R. (2009). Combining Data from Probability and Non-Probability Samples Using Pseudo-Weights. Survey Practice 2(6). 1-6.
- Kruskal, W., and Mosteller, F. (1980). Representative Sampling, IV: the History of the Concept in Statistics, 1895-1939. International Statistical Review 48(1). 169-195.
- Lazer, D.M., Kennedy, R., King, G., and Vespignani, A. (2014). The Parable of Google Flu: Traps in Big Data Analysis. Science 343. 1203-1205.
- Little, R.J.A., and Rubin, D.B. (2002). Statistical Analysis with Missing Data. 2nd edition. Hoboken: John Wiley & Sons.
- Lohr, S.L. (2010). Sampling: Design and Analysis. 2nd edition. Boston: Brooks/Cole, Cengage Learning.
- Meng, X.-L. (2018). Statistical Paradises and Paradoxes in big data (I): Law of large populations, big data paradox, and the 2016 US presidential election. The Annals of Applied Statistics 12(2). 685-726.
- Quatember, A. (2001). Die Quotenverfahren. Stichprobentheorie und -praxis. Aachen: Shaker Verlag. [in German]
- Quatember, A. (2019). The representativeness of samples (Chapter 48). In: Darquennes, J., Salmons, J., and Vandenbussche, W. (eds.). Handbook on Language Contact. Series Handbooks of Linguistics and Communication Science. Berlin: de Gruyter. Chapter 48. [in print]
- Särndal, C.-E., Swensson, B., and Wretman, J. (1992). Model Assisted Survey Sampling. New York: Springer.
- Schouten, B., Cobben, F., and Bethlehem, J. (2009). Indicators for the representativeness of survey response. Survey Methodology 35(1). 101–113.
- Tourangeau, R., Edwards, B., Johnson, T.P., Wolter, K.M., and Bates, N. (eds.) (2014). Hard-to-Survey Populations. Cambridge: Cambridge University Press.
- Weisberg, H.F. (2005). The Total Survey Error Approach. A Guide to the new Science of Survey Research. Chicago: The University of Chicago Press.




