Does name order still matter for candidates in a presidential primary poll in the US? Lack of response order effect in a web survey experiment
Liu, M. (2017). Does name order still matter for candidates in a presidential primary poll in the US? Lack of response order effect in a web survey experiment. Survey Methods: Insights from the Field. Retrieved from https://surveyinsights.org/?p=8217
The data used in this article is available for reuse from http://data.aussda.at/dataverse/smif at AUSSDA – The Austrian Social Science Data Archive.
The data is published under a Creative Commons Attribution 4.0 International License and can be cited as: Liu, Mingnan, 2017, “Replication Data for: ‘Does name order still matter for candidates in a presidential primary poll in the US? Lack of response order effect in a web survey experiment.’ Survey Methods: Insights from the Field.”, AUSSDA Dataverse, V1, doi:10.11587/DUUGBY
© the authors 2017. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0) 
Abstract
During elections, political polls provide critical data for the support each candidate receives. For that reason, the measurement of questions asking about candidate support has been receiving some research attention. As the online survey is increasingly becoming a widely used tool for public opinion and election polls, evaluation of the measurement error associated with this survey mode is of importance. This study examines whether a candidate name order effect exists in presidential primary election surveys in the US. The findings show that contrary to previous studies the order of names does not have a significant impact on the support candidates received.
Keywords
election polls, response-order effect, survey experiments, Web surveys
Copyright
© the authors 2017. This work is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0) 
Introduction
Political polls play a critical role in elections. There is an increasing use of polls in the American presidential election campaign and the polls contribute to driving the campaign narrative. Among the polls reported in media, an increasing number of them are switching to or relying more heavily on online polls. For example, both the Washington Post (2016) and the NBC News (2016) reported polling results from online polls for the 2016 U.S. presidential election. Give that, it becomes more important than ever for researchers and pollsters to have a good understanding of online polls in the political context. One of the fundamental questions for political polls is how to present the candidates’ names. In this study, I focus on the candidates running to be the Republican Party’s nominee for president in the 2016 elections in the United States and test the response order effect on the support candidates receive from survey respondents.
When responding to a visually presented question, such as a web survey, respondents are more likely to choose the response option listed at the top than at the bottom. This is known as the primacy effect. An explanation of this phenomena offers the satisficing theory (Krosnick, 1991; Schwarz, Hippler, & Noelle-Neumann, 1992). There are two main explanations for the primacy effect. First, when processing a list of visually displayed options, rather than carefully processing all options before reaching an answer, satisficers stop as soon as they encounter a reasonably good enough option, leaving the later options unconsidered. Another aspect of the theory argues that although respondents would like to consider carefully each option, their mental capacity may prevent them from doing so. As a result, the options residing early on a list are given deeper cognitive processing than the later options (Krosnick & Alwin, 1987). Both mechanisms suggest that the candidates shown early on a list will be at a relatively more advantageous position than candidates listed later.
Previous research supports this in an election context. A study finds that of the 118 races in Ohio in 1992, 48 percent show response order effect and over 80 percent of those effects were attributed to the primacy effect (Miller & Krosnick, 1998). Visser, Krosnick, Marquette and Curtin (2000) also report primacy effects from telephone polls conducted in the 1980s and 1990s. The previous studies focused on state or local elections. A study examining the ballot name order effect in the 1998 Democratic primary in New York City showed that the first position candidates received higher vote shares, and sometimes the difference is larger than the margin of victory (Koppell & Steen, 2004). King and Leigh (2009) examined the name order effect in Australia federal elections between 1984 and 2004, and found a higher vote share for the first position candidates than other candidates on the ballots. The effect is particularly larger for independents and minor parties. More recently, webber, Rallings, Borisyuk and Thrasher (2014) demonstrated ballot name order effect in British local council elections as well and the effects become larger as the number of seats and competing candidates increases. The current study further tested response order effect on presidential primary election support using a web survey experiment. Based on the evidence presented in previous studies, in this study, I expected that the candidate listed at the beginning of the response options would receive more support than the candidate listed at the end of the response options. On the other hand, as suggested by (Miller & Krosnick, 1998), even though candidate name order effect has been negatively correlated with campaign awareness and candidate name recognition, it is also entirely possible that no name order effect exists in presidential elections, given the massive media coverage and high name recognition of some presidential candidates compared to other names.
Design of experiment
In this study, I ranked the 16 Republican Party presidential candidates according to the CNN’s May 2015 poll (Appendix A). In addition to presenting the 16 candidates altogether in forward or reversed order, I also tested the order effect in conditions where only a subset of candidates were presented. In total, there were 10 conditions. Another way to look at the setup is to conceptualize the 10 conditions in 5 pairs as I will analyze 5 comparisons that each implement two different sorting orders of candidates. For simplicity, I refer to the design as one randomized experiment having 5 comparisons. The experiment implemented the following conditions:
Comparison 1
- Condition 1 (Top 1–5): The top 5 candidates were presented from 1 to 5.
- Condition 2 (Top 5–1): The top 5 candidates were presented from 5 to 1.
Comparison 2
- Condition 3 (Top 1–10): The top 10 candidates were presented from 1 to 10.
- Condition 4 (Top 10–1): The top 10 candidates were presented from 10 to 1.
Comparison 3
- Condition 5 (Top 1–5 + Bottom 1–5): The top 5 candidates were presented from 1 to 5 and the bottom 5 candidates were presented from 12 to16.
- Condition 6 (Top 5–1 + Bottom 5–1): The top 5 candidates were presented from 5 to 1 and the bottom 5 candidates were presented from 16 to 12.
Comparison 4
- Condition 7 (Top 6–15): The top 6–15 candidates were presented from 6 to 15.
- Condition 8 (Top 15–6): The top 6–15 candidates were presented from 15 to 6.
Comparison 5
- Condition 9 (Full list 1–16): All 16 candidates were presented from 1 to 16.
- Condition 10 (Full list 1–16): All 16 candidates were presented from 16 to 1.
All conditions also included “Would not vote” and “Other (please specify)” options and they all used the same question wording, which read “Here is a list of possible candidates for the Republican nomination for president in 2016. If the 2016 Republican presidential primary or caucus in your state were being held today, for whom would you vote?” Only Republican respondents were tested in this experiment because the number of candidates was far more than the number of Democrat candidates, which caused a greater concern for response order effect. Of course, this is not to say that short scales are free of order effect, as demonstrated elsewhere (Holbrook, Krosnick, Moore, & Tourangeau, 2007). Also, given the large number of Republican candidates, shortening the list of response options by presenting only a subset of the candidates was appealing to the internal research team but it is important to ensure that shortening the list of candidates does not alter the survey estimates and create a response order effect in its own. The decision to limit the experiment to Republican candidates was for practical reasons. This is a limitation of the study and I address this further in the discussion.
The experiment was conducted using SurveyMonkey, an online survey platform, from July 2 to 13, 2015. At the end of each survey, the platform displays a webpage which is sometimes referred to as the survey Thank You page. The survey invite for this study was displayed on the Thank You page on various other surveys. Every day, there are about three million surveys completed on the platform. There was no control over which user-created surveys the invitation was displayed to or who saw the invitation. Therefore, this was a convenience sample and the response rate could not be calculated. Also, the information prior to this experiment, including the content of the prior survey and the survey responses, was not disclosed due to privacy reason. Recruiting at the end of other surveys into survey experiments is not uncommon (see e.g., Liu, Kuriakose, Cohen, & Cho, 2015). In total, there were 147,769 unique visits of the survey invitation page; among those, 16,772 clicked on the survey and 12,142 respondents completed the survey. No incentive was provided to the respondents. In the survey, respondents were asked to choose their party identification from “Republican”, “Democrat”, or “Independent”. Those that selected “Independent” received a further question asking whether they lean towards Republican, Democrat or Independent. Of all completed respondents, 3,170 were self-identified Republicans and 1,905 were independents that lean towards Republican. Thus, the total sample size for the experiment was 5,075. Eligible participants were randomly assigned to one of the 10 conditions. The eligible participants tended to be male, aged 45–64, white, and with a college education and above (appendix B). A check of the randomization shows that the demographic compositions are similar across all 10 conditions and they do not differ significantly.
Results
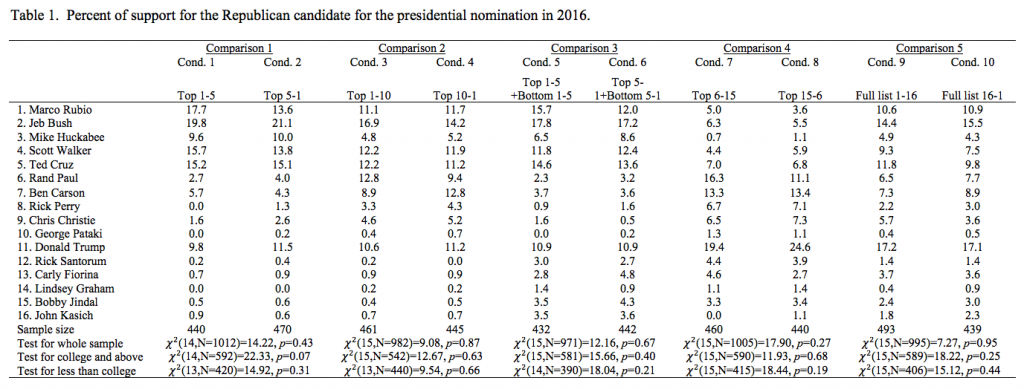
Table 1 presents the percentage of support for each candidate under each condition, regardless of whether their names were shown or not. Respondents were able to support unlisted candidates by entering their name in an open-text field at the bottom of the list (see questionnaire in the appendix). When comparing Condition 1 (Top 1–5) with Condition 2 (Top 5–1), the percentage of support for each candidate is very similar and the overall distributions are not significantly different from each other ( ![]() 2[14, n=1012]=14.22, p=0.43). Similarly, as the bottom of Table 1 shows, none of the p-values are significant based on the conventional 0.05 threshold, which suggests that no noteworthy response order effect exists in this experiment. To check whether there are differences for different levels of education I computed sub-group analyses. The last two rows of Table 1 present the chi-square test for the candidate name order effect by respondents’ education level. Similar to the whole sample analysis, for both more educated (college education or above) and less educated (less than college education) respondents, none of the five pairs of name orders are significantly different. Power analysis shows that the experiment has enough power (power=0.99) to detect a small difference (effect size=0.2) for each pair of conditions for the whole sample. For the college and above subgroup, the statistical power is at least 0.86 and for the below college group, the statistical power is at least 0.70. Therefore, the lack of significant difference for the whole sample and college and above subgroup is not the result of lack of statistical power. For the below college subgroup, I cannot entirely rule out that the smaller power is part of the reason for lack of significant difference.
2[14, n=1012]=14.22, p=0.43). Similarly, as the bottom of Table 1 shows, none of the p-values are significant based on the conventional 0.05 threshold, which suggests that no noteworthy response order effect exists in this experiment. To check whether there are differences for different levels of education I computed sub-group analyses. The last two rows of Table 1 present the chi-square test for the candidate name order effect by respondents’ education level. Similar to the whole sample analysis, for both more educated (college education or above) and less educated (less than college education) respondents, none of the five pairs of name orders are significantly different. Power analysis shows that the experiment has enough power (power=0.99) to detect a small difference (effect size=0.2) for each pair of conditions for the whole sample. For the college and above subgroup, the statistical power is at least 0.86 and for the below college group, the statistical power is at least 0.70. Therefore, the lack of significant difference for the whole sample and college and above subgroup is not the result of lack of statistical power. For the below college subgroup, I cannot entirely rule out that the smaller power is part of the reason for lack of significant difference.
However, it is possible that the response order effect only exists for the candidates’ names that were explicitly presented but not for the names that were offered by the respondents in “Other (please specify)”. For example, when comparing Condition 1 (Top 1-5) with Condition 2 (Top 5-1), the response order effect may only exist for the top 5 candidates but not for candidates 6 through 16, since their names are not presented in any order. To test whether this is the case, I examined the response order effect only for the candidates that were shown in the question. Other candidates whose names were offered by the respondents were coded to missing. The results are similar to Table 1. Specifically, none of the comparisons in this analysis, including Condition 1 with Condition 2 (![]() 2[4, n=1012]=2.65, p=0.61), Condition 3 with Condition 4 (
2[4, n=1012]=2.65, p=0.61), Condition 3 with Condition 4 (![]() 2[9, n=982]=7.96, p=0.53), Condition 5 with Condition 6 (
2[9, n=982]=7.96, p=0.53), Condition 5 with Condition 6 (![]() 2[9, n=971]=6.95, p=0.64), and Condition 7 with Condition 8 (
2[9, n=971]=6.95, p=0.64), and Condition 7 with Condition 8 (![]() 2[9, n=1005]=9.74, p=0.37), are significant. The comparison between Condition 9 and Condition 10 is the same as shown in Table 1 since all 16 candidates are presented. These findings once again confirm that the response order effect is not detectable in the experiment. The same analysis was conducted for the two education groups. For respondents with a less than college education, the analyses for Condition 1 against Condition 2 (
2[9, n=1005]=9.74, p=0.37), are significant. The comparison between Condition 9 and Condition 10 is the same as shown in Table 1 since all 16 candidates are presented. These findings once again confirm that the response order effect is not detectable in the experiment. The same analysis was conducted for the two education groups. For respondents with a less than college education, the analyses for Condition 1 against Condition 2 (![]() 2[4, n=268]=0.79, p=0.94), Condition 3 against Condition 4 (
2[4, n=268]=0.79, p=0.94), Condition 3 against Condition 4 (![]() 2[9, n=327]=7.34, p=0.60), Condition 5 against Condition 6 (
2[9, n=327]=7.34, p=0.60), Condition 5 against Condition 6 (![]() 2[9, n=273]=14.98, p=0.09), and Condition 7 against Condition 8 (
2[9, n=273]=14.98, p=0.09), and Condition 7 against Condition 8 (![]() 2[9, n=289]=13.27, p=0.15) indicate no candidate name order effect exists. For a college education and above respondents, the comparisons for Condition 1 with Condition 2 (
2[9, n=289]=13.27, p=0.15) indicate no candidate name order effect exists. For a college education and above respondents, the comparisons for Condition 1 with Condition 2 (![]() 2[4, n=421]=5.85, p=0.21), Condition 3 with Condition 4 (
2[4, n=421]=5.85, p=0.21), Condition 3 with Condition 4 (![]() 2[9, n=459]=10.09, p=0.34), Condition 5 with Condition 6 (
2[9, n=459]=10.09, p=0.34), Condition 5 with Condition 6 (![]() 2[9 ,n=429]=7.78, p=0.55), and Condition 7 with Condition 8 (
2[9 ,n=429]=7.78, p=0.55), and Condition 7 with Condition 8 (![]() 2[9, n=398]=4.32, p=0.88) also point to the lack of name order effect.
2[9, n=398]=4.32, p=0.88) also point to the lack of name order effect.
Discussion
Using a web survey experiment, I tested ten different versions of presenting Republican presidential candidates and one main finding emerged from the data: no response order effect exists for the Republican presidential candidates, regardless of the length of the list.
Although Miller and Krosnick (1998) find a primacy effect in elections, they also show that the effect is stronger when races have been minimally publicized. Respondents, or voters, are more likely to select a name listed on the top when a candidate’s name recognition is low. In the current study, this might not be the case for a presidential election. The order of the candidates’ names did not affect the results for a presidential primary election online poll. To the best of my knowledge, this is the first study that reveal a lack of name order effect. The United States Presidential election receives the most media coverage among all elections and the name recognition for many of the candidates is high for the general public. For the same reason, in the final election when it becomes a two-candidate race, the order of the names presented in the ballot should not be a factor influencing the outcome. This is a testable proposition and I encourage researchers to test this.
There are several limitations with this study and I encourage future research to examine them. First, future studies should examine whether an open-end question type without any options would elicit different results. Such a question type does not provide any hint or cue to the respondents and hence may result in a different conclusion. Second, additional work could also replicate this experiment in a telephone survey, as it is still the most popular mode for political polls. The effect of an interviewer reading a long list of responses may provide a different pattern between telephone (aural) and web (visual); therefore, a different pattern may emerge from telephone surveys. Third, it is not clear whether the results from this study is unique to the 2016 presidential election or whether it will be replicable in future elections. It is also unclear whether election polls in other countries will show a similar pattern. Fourth, this study focused only on the Republicans although Democrats and Independents could vote in a GOP primary in some states. Alternating the order of candidates presented may cause different response behavior for Democrats and Independent than Republicans. Future studies could replicate this experiment among Democrats and Independents as it will potential reveal more insights on partisan bias. This would reveal whether a shorter candidate list show a different response order effect than a longer list.
Appendix A CNN poll result
Appendix B Respondents demographics by experimental conditions
Appendix C Screen shots for experimental conditions
References
- CBS News. (2015). Hillary Clinton extends Iowa lead, narrows Sanders’ lead in NH. Retrieved from http://www.cbsnews.com/news/clinton-extends-iowa-lead-amid-strong-ratings-on-commander-in-chief. November 23, 2015.
- Holbrook, A. L., Krosnick, J. A., Moore, D., & Tourangeau, R. (2007). Response Order Effects in Dichotomous Categorical Questions Presented Orally The Impact of Question and Respondent Attributes. Public Opinion Quarterly, 71(3), 325–348.
- King, A., & Leigh, A. (2009). Are ballot order effects heterogeneous? Social Science Quarterly, 90(1), 71–87.
- Koppell, J. G., & Steen, J. A. (2004). The effects of ballot position on election outcomes. Journal of Politics, 66(1), 267–281.
- Krosnick, J. A. (1991). Response strategies for coping with the cognitive demands of attitude measures in surveys. Applied Cognitive Psychology, 5(3), 213–236.
- Krosnick, J. A., & Alwin, D. F. (1987). An evaluation of a cognitive theory of response-order effects in survey measurement. Public Opinion Quarterly, 51(2), 201–219.
- Liu, M., Kuriakose, N., Cohen, J., & Cho, S. (2015). Impact of web Survey Invitation Design on Survey Participation, Respondents, and Survey Responses. Social Science Computer Review, 894439315605606. https://doi.org/10.1177/0894439315605606
- Miller, J. M., & Krosnick, J. A. (1998). The Impact of Candidate Name Order on Election Outcomes. The Public Opinion Quarterly, 62(3), 291–330.
- Schwarz, N., Hippler, H.-J., & Noelle-Neumann, E. (1992). A cognitive model of response-order effects in survey measurement. In Context effects in social and psychological research (pp. 187–201). Springer. Retrieved from http://link.springer.com/chapter/10.1007/978-1-4612-2848-6_13
- Visser, P. S., Krosnick, J. A., Marquette, J., & Curtin, M. (2000). Improving election forecasting: Allocation of undecided respondents, identification of likely voters, and response order effects. Election Polls, the News Media, andDdemocracy. New York, NY: Chatham House.
- Webber, R., Rallings, C., Borisyuk, G., & Thrasher, M. (2014). Ballot order positional effects in British local elections, 1973–2011. Parliamentary Affairs, 67(1), 119–136.